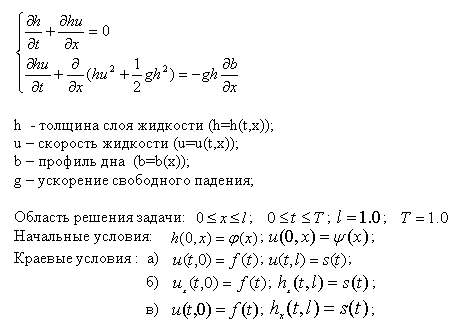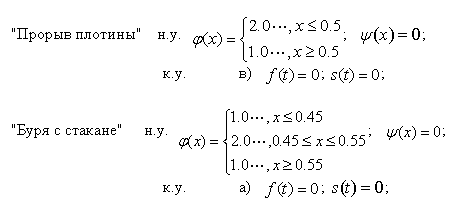Лекторы

К.ф.-м.н., доцент, Иванов Игорь Эдуардович, ivanovmai@gmail.com , 8(495)9392741.

К.ф.-м.н., н.с. , Коротеева Екатерина Юрьевна,  koroteeva@physics.msu.ru , 8(495)9392741.

Аннотация дисциплины

 В последние годы широкое развитие получили вычислительные методы для исследования многих задач физики и в частности задач механики сплошной среды.

В лекционном курсе содержатся базовые знания о способах решения задач механики сплошной среды с помощью постановки вычислительного эксперимента   и с использованием средств вычислительной техники. Основной упор сделан на рассмотрение задач гидроаэродинамики и сложного теплообмена. Целью курса является знакомство с вопросами построении математических моделей различных физических явлений, изучение основных методов исследования, возникающих при этом математических задач, выяснение физического смысла полученных решений. В рамках курса студенты знакомятся с особенностями комплексного решения нелинейных физических проблем в области механики сплошной среды, с корректной постановкой дополнительных условий на границах расчетной области, осваивают современные численные методы решения задач нестационарной динамики сжимаемых сред.

Цели освоения дисциплины

Целью курса является знакомство студентов с вопросами построения математических моделей различных физических явлений, изучение основных методов исследования, возникающих при этом математических задач, выяснение физического смысла полученных решений. В рамках курса студенты знакомятся с особенностями комплексного решения нелинейных физических проблем в области гидромеханики, с корректной постановкой дополнительных условий на границах расчетной области.

Задачи дисциплины

Дисциплина должна сформировать у выпускников по направлению знания и умение применять современные вычислительные методы к физическим задачам, традиционно рассматриваемым в разделах математической физики и механике сплошной среды. В практической ее части предполагается освоение слушателями программирования на базе языков высокого уровня.

    Дать студентам базовые знания по применению численных методов в решении задач математической физики, приобретение практических навыков численного решения задач гидрогазодинамики.

Компетенции

       Компетенции, необходимые для освоения дисциплины - ИК-3, ОНК-6

      Компетенции, формируемые в результате освоения дисциплины - ИК-4, ПК-2.

 Требования к результатам освоения содержания дисциплины

 В результате освоения дисциплины обучающийся должен получить представление об основных математических моделях описания движущихся газовых сред, в том числе течений с разрывами; об основных математических методах решения систем уравнений лежащих в основе этих моделей, о корректной постановке краевых условий на границе рабочей области. Освоить полуаналитические_методы решения упрощенных задач гидродинамики и современные численные методы решения задач гидромеханики сжимаемых сред в многомерных областях сложной геометрии.

Содержание и структура дисциплины

Место дисциплины в структуре ООП ВПО

1. Спецкурс кафедры (по выбору).
2. Вариативная часть, блок В-ПД.
3. Является основой для чтения дисциплин кафедры молекулярной физики. Необходимо знание математического анализа, аналитической геометрии, теоретической механики.

• Математический анализ, линейная алгебра, дифференциальные уравнения, теория функции комплексного переменного, механика сплошных сред, физическая газодинамика, уравнения математической физики, численные методы.
• Освоение курса необходимо для выполнения научно-исследовательской практики, научно-исследовательской работы, дипломной работы и   освоения спецкурсов, тематика которых связана с использованием математического моделирования задач механики сплошной среды и проведения вычислительного эксперимента.

Образовательные технологии

Учебный процесс состоит из двух частей лекционного материала и практикума, который студенты выполняют самостоятельно в виде сквозного домашнего задания. Контрольные работы так же привязаны к материалу практикума. Практикум выполняется с использованием компьютеров. В результате студентами самостоятельно реализуется полный цикл проведения вычислительного эксперимента для модельной задачи вычислительной гидродинамики.

Оценочные средства для текущего контроля успеваемости и промежуточной аттестации

Примеры:

- Контрольная работа №1 по теме Численные методы решения уравнений математической физики

       2. В системе

 - Контрольная работа №2 по теме Численные методы решения задач газовой динамики.

 вариант №1

 Провести часть характеристического анализа (найти собственные значения – характеристические скорости) системы уравнений из задания практикума (РГЗ) пункт 1.

- задание из практикума (домашнего задания) к курсу:

вариант №1

Задана квазилинейная система уравнений: Мелкой воды, описывающая неустановившееся течение в тонком слое (пленке) жидкости

1. Провести характеристический анализ. Определить тип уравнения. Получить характеристическую систему уравнений.
2. Реализовать алгоритм и программу решения задачи сеточно-характеристическим методом.
3. Реализовать алгоритм и программу решения задачи методом Годунова.
4. Реализовать алгоритм и программу решения задачи методом крупных частиц.
5. Провести вычислительные эксперименты для двух задач:

- полный перечень вопросов к зачёту;

Схема вычислительного эксперимента. Типы физических моделей. Характерные задачи (ВГД). Основные понятия и определения. Основные принципы, постулаты, гипотезы.. Плоское безвихревое движение несжимаемой жидкости. Потенциал скорости, Функция тока. Связь функции тока с потенциалом скорости. Комплексная скорость и комплексный потенциал. Использование комплексного потенциала для описания безвихревого движения несжимаемой жидкости. Примеры комплексного потенциала: однородный поток, течение от источника и стока, вихрь, дублет, вихреисточник. Комплексный потенциал ряда источников (стоков), ряда дублетов. Циркуляция скорости. Бесциркуляционное обтекание цилиндра равномерным плоскопараллельным потоком идеальной жидкости. Циркуляционное обтекание цилиндра равномерным плоскопараллельным потоком идеальной жидкости. Поперечная (подъемная) сила. Эффект Магнуса, Роторы Флетнера. Формулы Чаплыгина для гидродинамических реакций . Формула Жуковского для подъемной силы . Парадокс Даламбера Вихревое движение. Вихревые линии и вихревые трубки. Уравнение Эйлера. Уравнение движения в форме Громека-Лемба. Первые интегралы движения идеальной жидкости. Интеграл Бернулли и его приложения. Вихревые движения идеальной жидкости. Теорема Стокса. Теоремы Томпсона и Лагранжа о возможности вихревых движений. Метод дискретных вихрей. Линейные уравнения второго порядка с 2-мя независимыми переменными относительно одной функции. Характеристическое уравнение. Характеристики. Классификация. Корректность постановки задач математической физики. Решение Даламбера для гиперболического уравнения . Области зависимости и влияния. Линейное уравнение в частных производных первого порядка – уравнение переноса. Нелинейное (квазилинейное) уравнение переноса. Уравнение Бюргерса. Нелинейные эффекты. Разрывные решения гиперболических задач. Обобщенные решения. Соотношения на разрывах. Вычислительные сетки. Основные понятия теории разностных схем. Метод характеристик для квазилинейной гиперболической системы. Постановка граничных условий с использованием метода характеристик. Прямой метод характеристик. Послойный метод характеристик, вывод разностных соотношений. Численные схемы решения параболических уравнений (уравнения диффузии, теплопроводности. Численные схемы решения эллиптических уравнений. Постановка граничных условий на криволинейных границах. Методы контрольного объема (на примере решения системы уравнений нестационарной одномерной газовой динамики). Соотношения на разрывах в газовой динамике. Метод Годунова первого порядка. Граничные условия и их реализация. Задача о распаде произвольного разрыва (задача Римана). Метод крупных частиц

Учебно-методическое обеспечение дисциплины

Основная литература

1. Федорченко Р.П. Введение в вычислительную физику. М.: Изд-во Моск. физ. -техн. ин-та, 1994 г. - 528 с.
2. Лойцянский Л.Г. Механика жидкости и газа М., Л., 1976.
3. Куликовский Э, Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: Физматлит, 2001.
4. Флетчер К. Вычислительные методы в динамике жидкости Т.1, Т.2 , М.:Мир, 1991.
5. Андерсон Д., Таннехил Дж., Плетчер Р., Вычислительная гидромеханика и теплообмен. Т.1, Т.2 , М.:Мир, 1990.
6. Оран Э., Борис Дж. Численное моделирование реагирующих потоков. М.: Мир 1990.

Дополнительная

1. Роуч П. Вычислительная гидромеханика.       М.:Мир, 1980, 616с.
2. Годунов С.К., Забродин А.В., Иванов М.Я., Крайко А.Н., Прокопов Г.П.       Численное решение многомерных задач газовой динамики. М.: Гл.ред.физ.-мат.лит. 1976.
3. Поттер Д. Вычислительные методы в физике. М.:Мир, 1975.
4. Зализняк В.Е. Основы вычислительной математики. Часть 1. М.-Ижевск. 2004.
5. Белоцерковский О.М., Давыдов Ю.М. Метод крупных частиц в газовой динамике.М.: Наука. Главная редакция физико-математической литературы, 1982. - 392 с.

Интернет-ресурсы

http://molphys.phys.msu.ru

Полезная по тематике курса информация расположена по адресу:

www.cfd-online.com

Материально-техническое обеспечение

В соответствии с требованиями п.5.3. образовательного стандарта МГУ по направлению подготовки «Физика».

Аудитория 2-44.

В наличии есть проектор и компьютер для презентации. Практическая часть занятий проводится с использованием личных ноутбуков учащихся.